Tree
나무를 뒤집어 놓은 것처럼 하나의 시작 노드로부터 자식 노드들이 파생되는 자료 구조다.
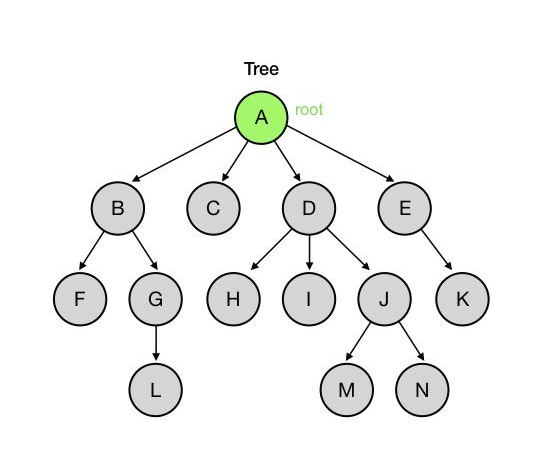
- 트리는 항상 root부터 시작해서 아래로 가지치기를 한다.
- 트리 구조는 그래프의 한 종류로 단일한 방향성을 가지며 원형 구조(순환구조)로는 존재하지 않는다.
- 하나의 노드에는 하나 이상의 차일드 노드가 붙을 수 있다.
- HTML의 구조가 좋은 예시가 된다.
- 관련 용어들
- Root : 시작하는 노드를 가리킨다. 하나의 트리에는 1개만 존재.
- Leaf : 자식 노드가 없이 트리의 가장 마지막에 위치한 노드를 말한다.
- Parent / Child : 연결된 상위 부모 노드를 parent, 하위 자식 노드를 child라고 한다.
- Edge/Branch: 노드와 노드의 연결 선
- Path: 노드 간의 연결
- Children / Sibling: 부모 노드 아래로 파생된 모든 노드는 children에 담겨있다. 같은 부모 노드를 가지고 있는 자식 노드들은 서로의 sibling으로 본다.
- Height: 부모 노드와 자식 노드 간의 edge의 개수를 말한다.
Tree의 Property(속성)
- value : 노드의 값
- children : 자식 트리
Tree의 Method(메서드)
- add child : child 노드를 추가한다
- remove : child 노드를 삭제한다
- contains : 트리가 해당 노드 값을 가지고 있는지 탐색한다
- traverse : 모든 트리의 value를 callback 함수에 의해 변경한다.
- map : callback 함수에 의해 변경된 새로운 트리를 반환한다.
Pseudoclassical Implementation
const Tree = function(value) {
this.value = value;
this.children = [];
}
Tree.prototype.addChild = function(value) {
const child = new Tree(value);
this.children.push(child);
}
Tree.prototype.contains = function(target) {
if(this.value === target) {
return true;
}
for(let i = 0; i < this.children.length; i++) {
const child = this.children[i];
if(child.contains(target)) {
return true;
}
}
return false;
}
Tree.prototype.traverse = function(callback) {
callback(this.value); //기존의 값을 넣는다
if(!this.children){
return;
}
for(let i = 0; i < this.children.length; i++) {
const child = this.children[i];
child.traverse(callback;)
}
}
Tree.prototype.map = function(callback) {
const newTree = new Tree(); //새로운 트리를 만든다
newTree.value = callback(this.value);
newTree.children = this.children.map(function(child) {
return child.map(callback)
});
return newTree;
}
Binary Search Tree(BST)
트리는 형태에 따라서 종류를 구분한다. 노트에 차일드가 최대 2개까지 붙는 트리를 바이너리 트리(Binary tree)라고 한다.
바이너리 트리 중에서도 트리의 데이터가 노드를 기준으로 왼쪽은 작은 값을, 오른쪽은 큰 값을 가지고 있는 트리를 바이너리 서치 트리 (Binary search tree), 또는 이진 탐색 트리라고 한다.

- 각 노드의 왼쪽 서브트리는 해당 노드의 값보다 작거나 같은 값을 가진다.
- 각 노드의 오른쪽 서브트리는 해당 노드의 값보다 큰 값을 가진다.
- 왼쪽과 오른쪽의 서브트리는 또한 각각 이진 탐색 트리의 형태를 유지하고 있다.
- 어떤 값을 찾을 때 root 에서부터 두 갈래 길을 선택해서 가다 보면 그 값을 찾을 수 있다. 찾으려는 값과 비교해서 작으면 왼쪽, 크면 오른쪽으로 내려가면서 탐색한 다.
DFS와 BFS
바이너리 서치 트리를 순화하는 방법에는 DFS(깊이 우선 탐색, Depth-First Search)와 BFS(너비 우선 탐색, Breadth-First Search) 두 가지가 있다.
- DFS : 루트를 시작으로 점차 깊이 들어갔다가 가장 깉은 depth에 도달했을 때 다시 나오고, 또다시 깊이 들어가는 방식을 반복하며 전체 트리를 순회한다.
- BFS : sibling을 먼저 탐색하고, 그 후 다음 depth로 들어가 해당 depth의 sibling을 탐색하는 식으로 전체 트리를 순회한다.

Binary Tree Traversals(트리의 3가지 순회방법)
바이너리 트리는 순회 방법에 따라 테이터 출력 순서가 달라진다.
아래 세 가지 검색 방법은 모두 깊이 우선 검색(Depth-First Search : DFS)에 속한다.
- Inorder : Left - Root - Right 순으로 탐색
- Preorder : Root - Left - Right
- Postorder : Left - Right - Root

BST의 Property(속성)
- value : 노드의 값
- left : 왼쪽 자식 노드
- right : 오른쪽 자식 노드
BST의 Method(메서드)
- insert : child노드를 추가한다
- contains : 트리가 해당 노드 값을 가지고 있는지 탐색한다
- dfs : 깊이 우선 탐색 시의 데이터를 출력한다.
- bfs : 너비 우선 탐색 시의 데이터를 출력한다.
Class Implementation
class Node {
constructor(value) {
this.value = value;
this.left = null;
this.right = null;
}
}
class BST {
constructor(value) {
this.root = new Node(value);
}
insert(value) {
let newNode = new Node(value)
const searchTree = node => {
if (value < node.value) {
if (!node.left) {
node.left = newNode;
} else {
searchTree(node.left);
}
}
else if (value > node.value) {
if (!node.right) {
node.right = newNode;
} else {
searchTree(node.right);
}
}
}
searchTree(this.root)
}
contains(target) {
let currentNode = this.root;
while (currentNode) {
if (target === currentNode.value) {
return true;
}
if (target < currentNode.value) {
currentNode = currentNode.left
} else {
currentNode = currentNode.right
}
}
return false;
}
dfsInOrder() {
let result = [];
const traverse = node => {
if (node.left) traverse(node.left)
result.push(node.value)
if (node.right) traverse(node.right)
}
traverse(this.root);
return result;
}
dfsPreOrder() {
let result = [];
const traverse = node => {
result.push(node.value)
if (node.left) traverse(node.left)
if (node.right) traverse(node.right)
}
traverse(this.root);
return result;
}
dfsPostOrder() {
let result = [];
const traverse = node => {
if (node.left) traverse(node.left)
if (node.right) traverse(node.right)
result.push(node.value)
}
traverse(this.root);
return result;
}
bfs() {
let result = [];
let queue = [];
queue.push(this.root);
while (queue.length) {
let currentNode = queue.shift()
result.push(currentNode.value)
if (currentNode.left) {
queue.push(currentNode.left)
}
if (currentNode.right) {
queue.push(currentNode.right)
}
}
return result;
}
}
레퍼런스 :
'Coding > TIL (Today I Learned)' 카테고리의 다른 글
| [Javascript] 논리연산자를 이용한 변수 초기화 (0) | 2019.12.17 |
|---|---|
| [JavaScript] Recursion (재귀) (0) | 2019.12.14 |
| Data Structure 02: (0) | 2019.12.09 |
| OOP 02: JavaScript의 Prototype (0) | 2019.12.08 |
| Data Structure 01: Stack & Queue (0) | 2019.12.07 |
