Complexity Analysis(복잡도 분석)
복잡도란 알고리즘이 문제를 해결하는 데 있어서 시간(time complexity)과 공간(space complexity)을 얼마나 차지하는지를 나타내는 지표이다. 여기서 공간 복잡도는 코드를 저장하고 수행하기 위한 시스템 공간 등을 의미한다.
시간과 공간의 복잡도는 왜 중요할까? 시간과 공간의 복잡도가 그 알고리즘이 얼마나 효율적인지를 나타낼 수 있기 때문이다.
시간과 공간이라는 자원이 무한정이라고 가정한다면 이 복잡도라는 것은 의미가 없다. 심지어 알파고 조차도 플레이 가능한 모든 가짓수를 계산해서 넣는다면 거의 무한에 가까운 경우의 수가 나온다고 해도 언젠가는 가능할 것이기 때문이다. 하지만 현실적으로는 불가능한 일.
Time complexity
이 포스트에서는 시간 복잡도에 한해 정리해보기로 한다.
알고리즘을 짤 때 주어진 문제를 어떻게든 해결하는 것을 최 우선순위로 두어야겠지만우리는 누구나 최대한 시간을 효율적으로 사용하고 싶어 한다. 시간 복잡도를 최소화하려는 노력도 같은 맥락이다.
Big-O Notation
Big-O 표기법은 알고리즘의 전체 단계를 대수 용어로 변환한 다음 문제의 전체 복잡성에 큰 영향을 미치지 않는 하위 상수 및 계수를 제외하는 방법이다. 하위 상수 및 계수를 제외한다는 것은 이런 식.
Regular Big-O
2 --> O(1) 고정된 값은 1로 표기
2n + 10 --> O(n) 2와 10은 삭제하고 n 으로 표기
5n^2 --> O(n^2) 5는 삭제하고 n^2 으로 표기
대표적으로 5가지 정도로 구분하는데 복잡도 순으로 예시 코드와 함께 보면 표기법을 이해하기 쉽다.
O(1) constant time
입력값 n이 주어졌을 때, 알고리즘이 문제를 해결하는 데 오직 한 단계만 거친다.
예시 : Array lookup, Hash table insertion
var array = [1, 2, 3, 4];
array.pop() // 4
O(log N) log time
입력값 n이 주어졌을 때, 문제를 해결하는데 필요한 단계 뜰이 연산마다 특정 요인에 의해 줄어든다.
예시 : Binary search(이진탐색)
function FindItemBinarySearch(items, match) {
var low = 0,
high = items.length - 1;
while (low <= high) {
mid = parseInt((low + high) / 2);
current = items[mid];
if (current > match) {
high = mid - 1;
} else if (current < match) {
low = mid + 1;
} else {
return mid;
}
}
return -1;
}
O(n) linear time
문제를 해결하기 위한 단계의 수와 입력값 n이 1:1 관계를 가진다.
예시 : Linked list
Array.prototype.indexOf = function(element) {
for (var x = 0, count = this.length; x < count; x++) {
if (this[x] === element) {
return x;
}
}
return -1;
};
O(n^2) quadratic time
문제를 해결하기 위한 단계의 수는 입력값 n의 제곱이다.
예시 : Two nested for loop(이중 포문)
const buildMatrix = (n) => {
var matrix = new Array(n);
for (var i = 0; i < n; i++) {
var cols = new Array(n);
matrix[i] = cols;
for (var j = 0; j < n; j++) {
cols[j] = j
}
}
return matrix
}
O(c^2) exponential time
문제를 해결하기 위한 단계의 수는 주어진 상수값 C의 n 제곱이다.
예시 : Recursion(메모이제이션을 쓰지 않은 재귀)
function fibonacci(num) {
var answer = 0;
if (num <= 1) {
return num;
}
else if (num > 1) {
answer = fibonacci(num - 1) + fibonacci(num - 2);
}
return answer;
}Big-O Functions ranking
O(1) -------- : Constant time Better
O(log n) --- : Log time
O(n) ------- : Linear time
O(n log n) -- : Log linear time
O(n^2) ----- : Quadratic time
O(n^3) ------: Cubic time
O(2^n) ----- : Exponential time Worse
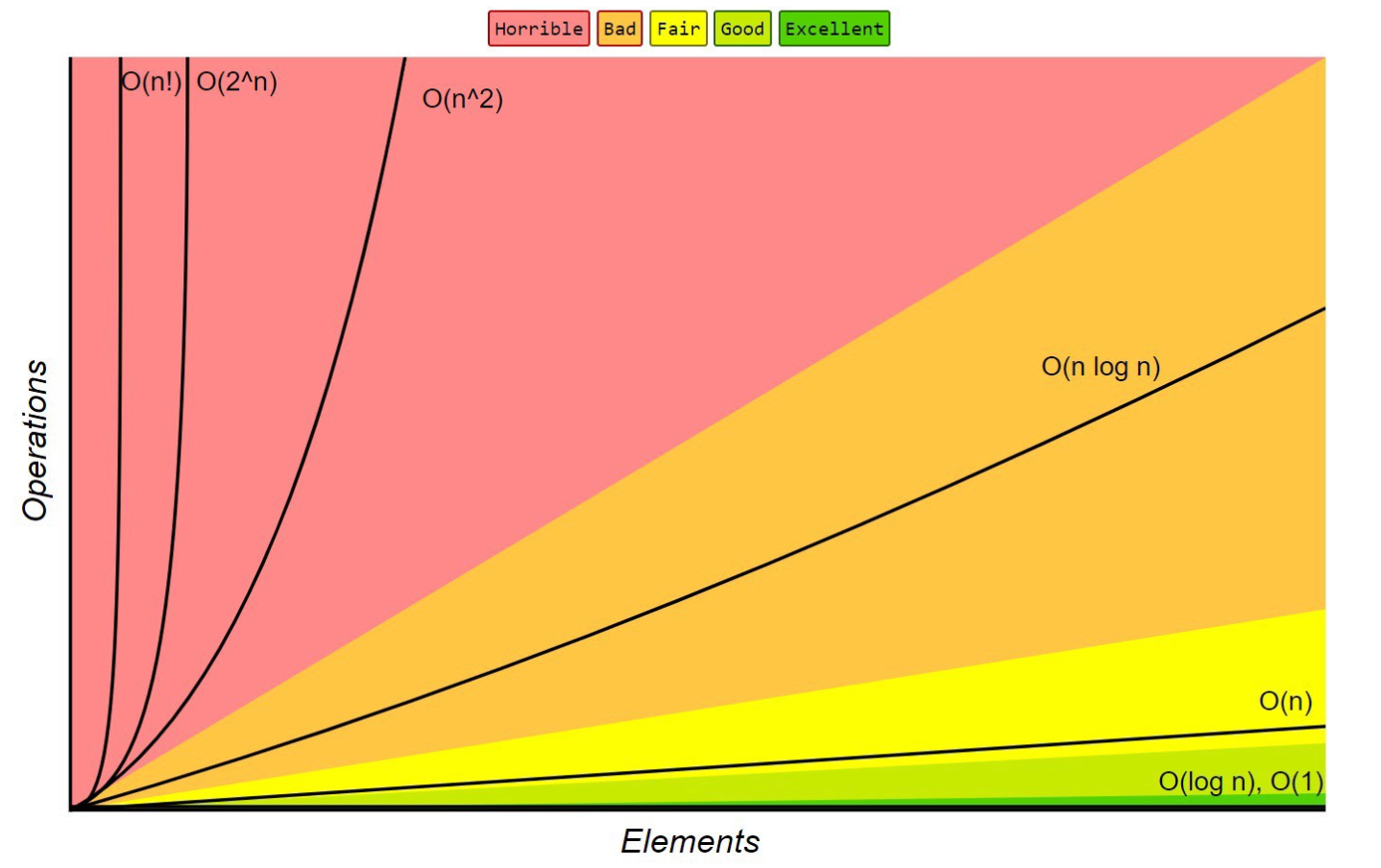
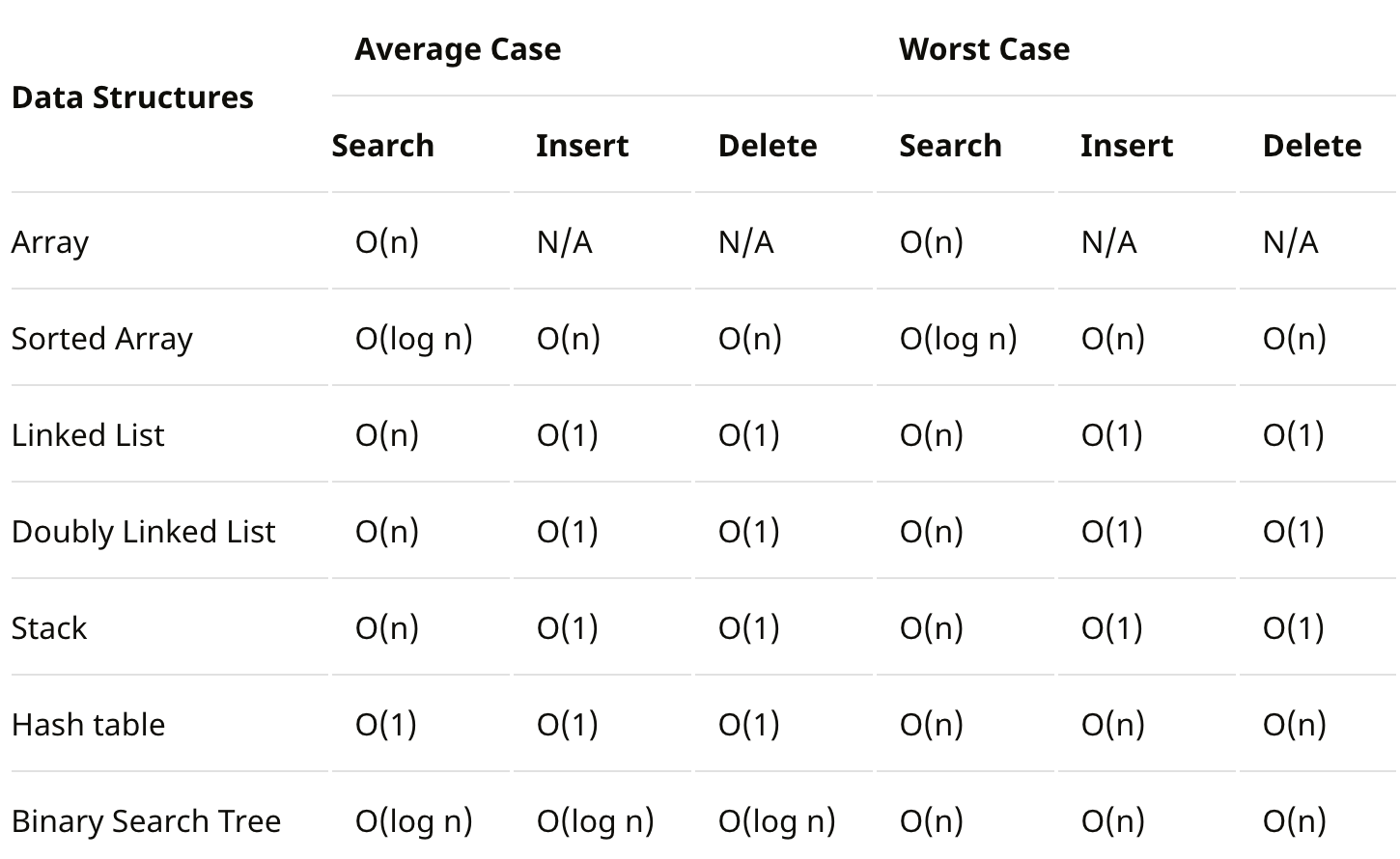
데이터 구조 별 Big-O
'Coding > TIL (Today I Learned)' 카테고리의 다른 글
| 브라우저는 어떻게 동작 할까 - Basic Web Architecture (0) | 2020.01.17 |
|---|---|
| 함수이름 앞에 언더바(_)를 쓰는 이유 (0) | 2020.01.15 |
| [JavaScript] This의 특징과 5가지 패턴 (0) | 2019.12.25 |
| Basic CSS: Units, box-sizing, position, float, display (0) | 2019.12.24 |
| [JavaScript] __proto__, constructor, prototype의 관계, 그리고 Class (0) | 2019.12.20 |

